- トップ
- 要素剛性マトリクスの導出
要素剛性マトリクスの導出
はじめに
図1,図2に示すような,三角形1次要素の要素剛性マトリクスを導出します。後述しますが三角形1次要素では仮定する変位分布は座標(x,y)の一次式で仮定します。この結果,応力とひずみは要素内で一定値をとなります。
説明を簡単にするために,二次元問題のひとつである平面応力状態で議論します。平面応力状態では6つの応力成分(σx,σy,σz,γxy,γyz,γzx)のうちσz,γyz,γzxがゼロとなります。
反時計回りにi,j,kと節点に名前を付けます。i節点について,座標を(xi,yi),作用するx方向の力をfi,y方向の力をgi,x方向変位をui,y方向変位をviとします。j節点についてはそれぞれ(xj,yj),fj,gj,uj,vjとし,k節点についてはそれぞれ(xk,yk),fk,gk,uk,vkとします。そして板厚をhとします。
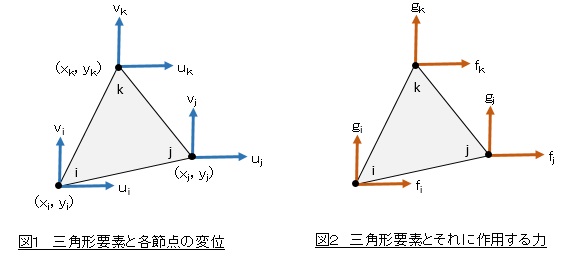
節点変位と節点に要する力の関係は次式となり,[k]が要素剛性マトリクスです。[k]はばね定数のようなものと解釈しております。
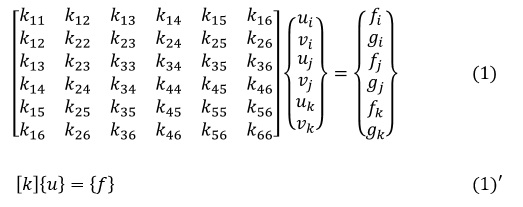
要素剛性マトリクス[k]と,[k]を合成して作られる全体マトリクス[K]には,以下の特徴があります。
- 正方マトリクスである。
- 対称マトリクスである。
- ある列について[K]の成分を合計するとゼロとなり,ある行についても[K]の成分を合計するとゼロとなる。
- [K]の対角成分は正である。
- [K]の逆マトリクスは存在しない。
これから,[k]の具体的な値を導きます。
弾性体の支配方程式
弾性体の支配方程式は,つり合い方程式,ひずみ-変位関係式,応力-ひずみ関係式から構成されます。以下に記します。
つり合い方程式は次式です。
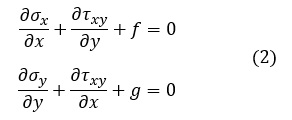
ここで,σx,σy,τxyは,座標(x,y)における応力成分,fは単位体積当たりに作用するx方向の外力,gはy方向の外力です。要素剛性マトリクスの導出では,つり合い方程式は使わず,その代わりに仮想変位の原理,ないしは,最小ポテンシャルエネルギの原理による式を使います。
ひずみ-変位関係式は次式です
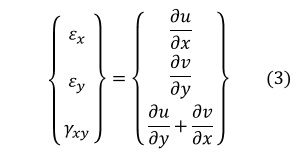
ここで,εx,εy,γxyは座標(x,y)におけるひずみ成分,u,vは座標(x,y)におけるx方向変位とy方向変位です。
応力-ひずみ関係式を説明する前に,二次元版一般化したフックの法則を説明します。ヤング率Eとポアソン比νの定義から,一般化したフックの法則は次式で表されます。
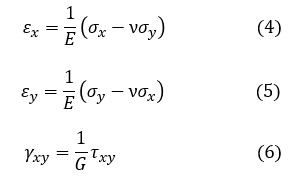
(4),(5)式をσx,σy,τxyについて解くと次式となります。
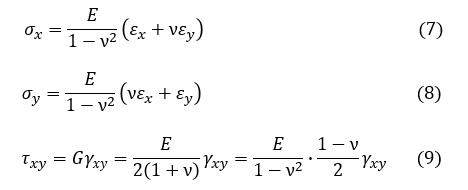
(7),(8),(9)式をマトリクス表示にすると次式となります。
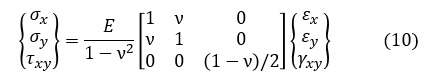
次式で定義されるマトリクス[D]を応力-ひずみマトリクスと呼ぶことにすると,応力ベクトル{σ}は(12)式で表記されます。
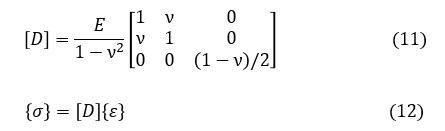
(10)式,(12)式が応力ーひずみ関係式です。
変位法
つり合い方程式,ひずみ-変位関係式,応力-ひずみ関係式を境界条件(変位拘束と外力)の下で解けば,未知数(σx,σy,τxy,εx.εy,γxy,u,v)を求まるはずですがこれがとても難しいので,少し簡単にします。ひずみ-変位関係式(3)式を応力ーひずみ関係式(10)式に代入し,さらにこれをつり合い方程式(2)式に代入すれば,未知数は変位u,vだけになります。このように変位だけに関する方程式にして解くやり方は,一般に変位法と呼ばれています。しかし変位u,vだけにしたとしても,方程式を解くにはまだまだ難しいです。ここで有限要素法の出番となります。有限要素法の基本となる式((1)式)の未知数は変位{u}ですので,ここで説明している有限要素法も変位法です。
変位の近似式(変位関数)
図3は表面の一部を固定し表面のある部分に外力が作用している連続体です。連続体の任意の点(x,y)の変位(u,v)を求める問題ですが,とても難しい問題であることは前述しました。ここで連続体を小さな要素に分割し,小さな要素の中では変位(u,v)を簡単なx,yの関数で表して近似してはどうでしょうか。近似ではありますが簡単な形なので,弾性体の支配方程式の近似解も簡単に求まりそうです。(u,v)の変化の激しいところでは要素分割を細かくすれば,よい近似ができそうです。近似式としては(13),(14)式のような形があります。この近似式を変位関数といいます。
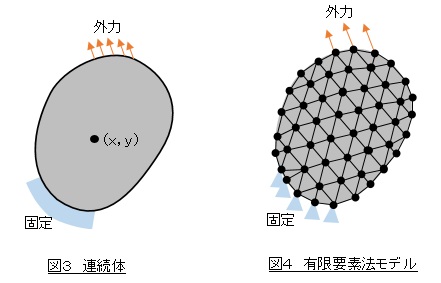
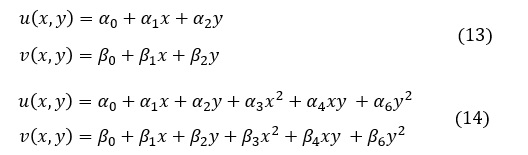
(13)式を使って要素剛性マトリクスを作ったものを三角形1次要素といい,三角形1次要素ではひとつの要素内の応力とひずみは一定値をとります,(14)式を使って要素剛性マトリクスを作ったものを三角形2次要素といい,三角形2次要素ではひとつの要素内の応力とひずみは1次式(線形)で変化します。
簡単な変位関数として(13)式,(14)式を例に出しましたが,他の形の変位関数も考えられます。変位関数に要求される条件を以下に記します。
1.真の解を十分よく近似できるものであること
2.物理的に正当でない関数を含まないこと。例えば,図3の連続な弾性体の内部で変位が不連続になるはずが
ないので,変位関数にも不連続関数が含まれていないこ。
3.幾何学的境界条件(変位の境界条件)を満たすことができること
4.各項が1次独立であること
5.微分や積分の計算が容易であること
(13)式,(14)式のような多項式の場合,上記2,4,5を満足しています。上記3については,要素の形状が凸多角形のように単純な形であれば問題ありません。今回は三角形なので問題ありません。1についてですが,多項式の次数をどんどん上げていくと真の解をより正確に表現できますので問題ありません。しかし,次数を上げると計算が複雑になるなどの他の弊害が出てくるので,次数は2次に抑えておき変化が急峻なところは要素分割を細かくする戦略をとることが多いです。
要素分割を細かくしていったら,有限要素法による計算結果が真の値に近づくかどうかには興味があります。真の値に収束する変位関数の条件は,文献3)によると以下のようになります。
1.節点変位が剛体変位の条件を満足するような場合に,要素内部でひずみを生じないこと
2.節点変位が一定ひずみ状態に与えるようなものであれば,変位関数は要素内において一定ひずみ状態を与える
ものであること
3.変位関数によって計算されるひずみは,要素と要素の間の境界面上で有限であること
(13)式,(14)式は上記条件を満足しています。
ここでは(13)式を使った三角形1次要素の要素剛性マトリクスを導出していきます。
ひずみ-変位関係式
(3)式によるとひずみは変位を偏微分したものですので,変位とひずみは密接な関係があります。変位-ひずみ関係式は次式で表されます。

ここで
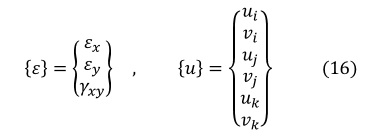
[B]は変位-ひずみマトリクスといい,3行6列のマトリクスです。これから(13)式をベースとして[B]の具体的な値を求めていきます。
図2に示したi,j,k節点の座標と変位を(13)式に代入します。
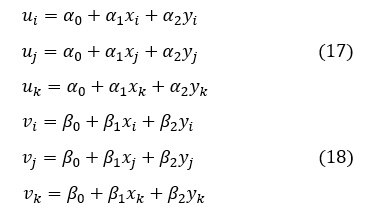
(17)式のα0,α1,α2を求めます。(17)式をマトリクス表示にすると次式になります。
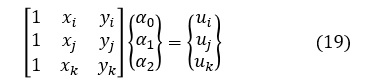
α0はクラメルの公式を使って次式で表されます。
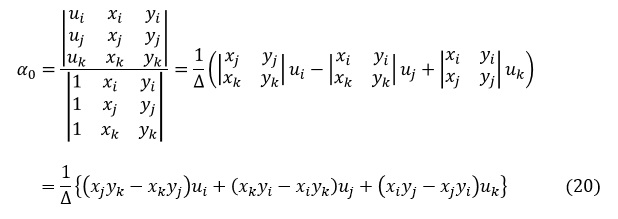
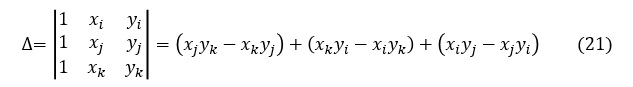
同様にα1は次式で表されます。
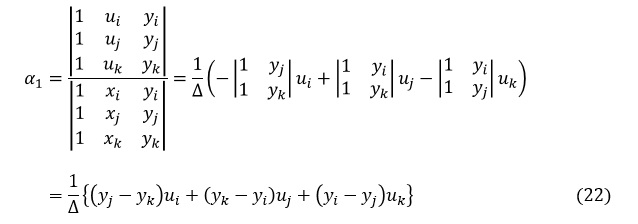
同様にα2は次式で表されます。
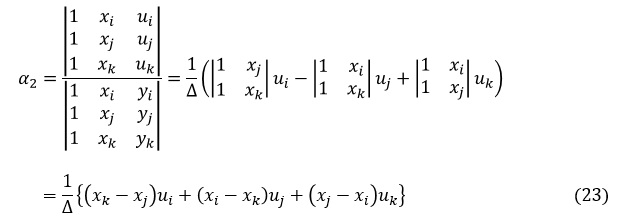
(20),(22),(23)式をマトリクス表示にすると次式となります。
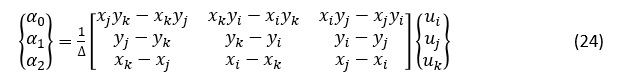
同様にして,β0,β1,β2を求めると次式となります。
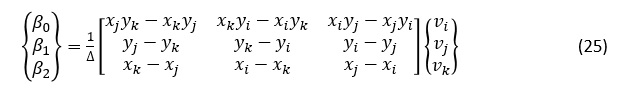
ひずみεx,εy,γxyを求めます。(3),(13),(24),(25)式からεx,εy,γxyは次式となります。
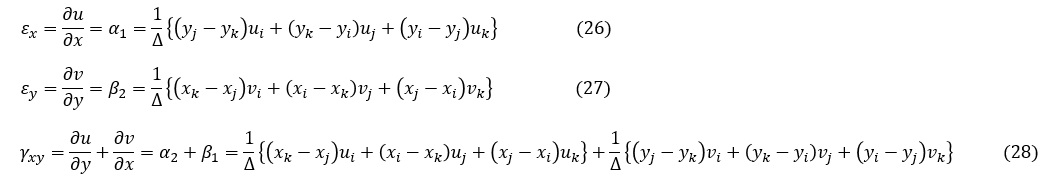
(26),(27),(28)式をマトリクス表示すると次式となります。
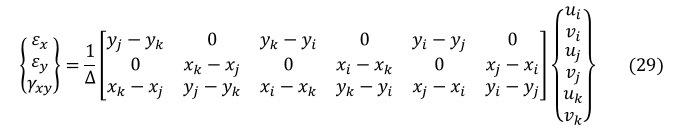
変位-ひずみマトリクス[B]は次式となります。
![変位-ひずみマトリクス[B]](img/c5_eq30.jpg)
[B]マトリクスは,定数だけから構成されることに注目してください。このことは後で要素剛性マトリクスを求めるときの積分操作が簡単になります。変位関数を(14)式のような2次式とすると,[B]マトリクスの中に座標x,yが入り,この積分操作で数値積分をする必要が生じます。
仮想仕事の原理
「ひとつの質点が,これに働くいくつかの力の作用の下でつり合い状態にあるとき,この質点に微小な仮想変位を与えても,質点に働いているすべての力がこの仮想変位によってなす仕事の総和はゼロである。」というのが仮想変位の原理(principle of virtual work)です。式で表すと次式になります。式の導出は仮想仕事の原理を参照ください。
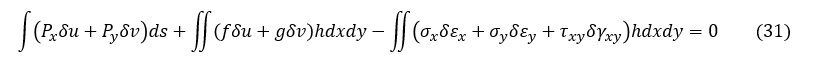
ここで,hは板厚,δu.δvは仮想変位,Px,Pyは単位面積当たりの表面力,f,gは単位体積当たりのx方向外力とy方向外力,δεx,δεy,δγxyは仮想変位の各成分δu.δvに対応するひずみ成分,です。δεx,δεy,δγxyは次式で表されます。
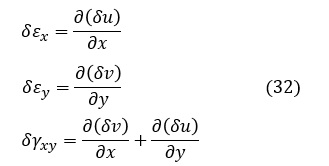
ここで,Px,Py,f,g,δu.δv,δεx,δεy,δγxy を以下のようにベクトル表示します。
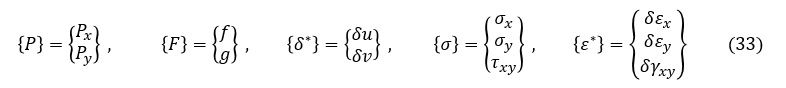
また,{δ*}Tは,{δ*}マトリクス(ベクトル)の転置マトリクスを表します。{ε*}Tも同様に転置マトリクスです。次式で表されます。
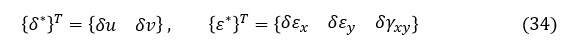
(31)式に(33)式,(34)式を代入すると,仮想変位の原理は次式で表すことができます。
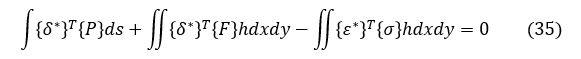
仮想仕事の原理は(2)式のつり合い方程式と等価であるため,
1)つり合い方程式
2)ひずみ-変位関係式
3)応力-ひずみ関係式
の代りに,
1)仮想仕事の原理
2)ひずみ-変位関係式
3)応力-ひずみ関係式
としても同じ解が得られます。
これから仮想仕事の原理から要素剛性マトリクスを導出します。
仮想仕事の原理を用いた要素剛性マトリクスの導出
今,体積力を考えないことにすると,(35)式は次式となります。
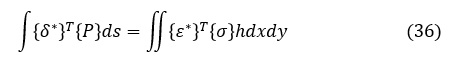
要素に作用する表面力{P}は三角形要素の各辺に作用し,δu,δvは三角形要素の各辺上の仮想変位ですが,連続体を要素分割したことに伴いこれらを離散化します。表面力{P}がなす仕事と離散化した節点力{f}がなす仕事が等しくなるように節点力{f}を定義します。離散化した節点での仮想変位と節点に作用している外力を(37)式のように表すことにすると,離散化した節点での仮想変位と節点に作用している外力がなす仕事は{δ*}T{f}となって,これが表面力{P}のなす仕事に等しいことになります。よって,(36)式の左辺は(38)式のようになります。
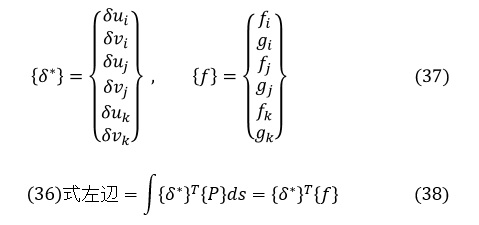
(36)式の右辺を変形していきます。
(12)式 {σ}=[D]{ε} を(36)式右辺に代入して
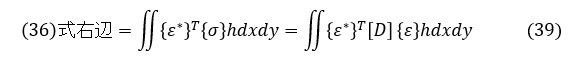
(15)式 {ε}=[B]{u} から,{ε*}と{ε}は次式となって
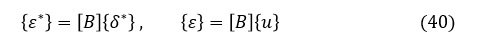
(40)式を(39)式に代入して,(36)式(仮想仕事の原理)の右辺は次式となります。
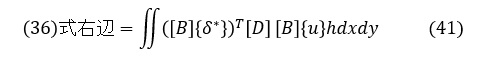
ここで,転置マトリクスの公式 ([A][B])T=[B]T[A]T を適用して
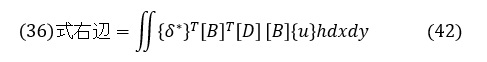
{δ*}T,{u},h は,座標(x,y)の関数でないため,積分の外に出して次式となります。
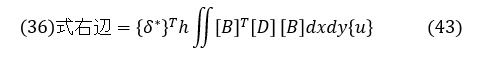
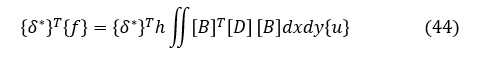
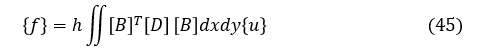
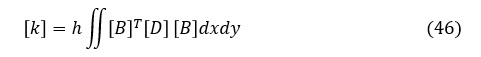
ここでは変位関数として(13)式を使用したことによって,[B]は(30)式で示したようにx,yの関数ではなく定数となるため,(46)式は次式となります。
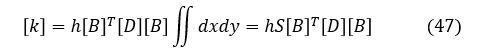
ここで,Sは三角形の面積です。
以上が要素剛性マトリクスの導出過程です。なんか狐につままれたようですね。仮想変位の原理はちょっとピンとこないところがありますので,以下に最小ポテンシャルエネルギの原理を用いて要素剛性マトリクスを導出してみます。
最小ポテンシャルエネルギの原理
「ポテンシャルエネルギの総和(全ポテンシャルエネルギ)が最小になる状態は,力の静的なつり合い状態である。」というのが最小ポテンシャルエネルギの原理です。
最小ポテンシャルエネルギの原理は(2)式のつり合い方程式と等価であるため,
1)つり合い方程式
2)ひずみ-変位関係式
3)応力-ひずみ関係式
の代りに,
1)最小ポテンシャルエネルギの原理
2)ひずみ-変位関係式
3)応力-ひずみ関係式
としても同じ解が得られます。
特に,弾性体に外力がかかり変形していて,変形の過程において外力の大きさと向きは一定であるとき,関与するポテンシャルエネルギは以下のものとなります。
弾性体のひずみエネルギ U
外部のポテンシャルエネルギ V
全ポテンシャルエネルギΠは両者の和であり,これが最小になる状態が力の静的なつり合い状態です。
二次元問題で考えると,弾性体のひずみエネルギUは,次式で表されます。
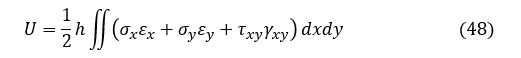
上式は,ばねに蓄えられるエネルギの式 U=(1/2)kx2=(1/2)kx・x=(1/2)力・変位 から類推できますね。
外部のポテンシャルエネルギVは,外力のした仕事の分だけ減少することになりますのでマイナスがついて,変形前の状態を基準(原点)にすれば,次式で表されます。
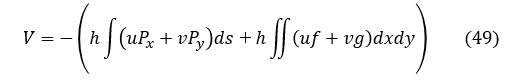
ここで,hは板厚,u,vは座標(x,y)におけるx方向変位,y方向変位,Px,Pyは単位面積当たりの表面力,f,gは単位体積当たりのx方向外力とy方向外力,です。
今,体積力を考えないことにすると,(49)式は次式となります。

全ポテンシャルエネルギΠは弾性体のひずみエネルギUと外部のポテンシャルエネルギVの和で次式で表されます。

Πが最小になる状態が静的平衡の状態であり,問題の解となります。
最小ポテンシャルエネルギを用いた要素剛性マトリクスの導出
(51)式の第1項 ひずみエネルギU を求めます。
今は図1,図2に示した三角形要素で,かつ(13)式で示した変位関数を用いているので,要素内の応力とひずみは座標(x,y)関数とはならず一定値です。よって,Sを三角形の面積とすれば(48)式のひずみエネルギは次式で表されます。
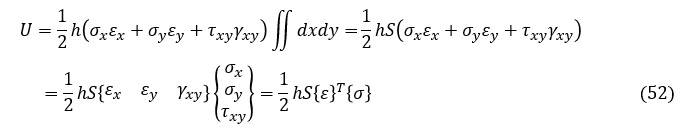
(52)式に(12)式と(15)式を代入すると次式になります。
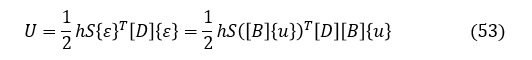
ここで,転置マトリクスの公式 ([A][B])T=[B]T[A]T を適用して
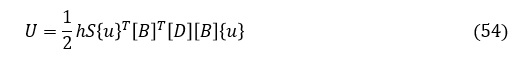
ここで,まだ[k]が要素剛性マトリクスと決まったわけではないのですが,

とおくと,ひずみエネルギは次式で表されます。

(51)式の第2項 外部のポテンシャルエネルギV を求めます。
図1,図2に示した三角形1次要素の場合,外力は,fi,gi,fj,gj,fk,gk で,これらに対応する変位は,ui,vi,uj,vj,uk,vk なので,(51)式の外部のポテンシャルエネルギVは次式で表されます。
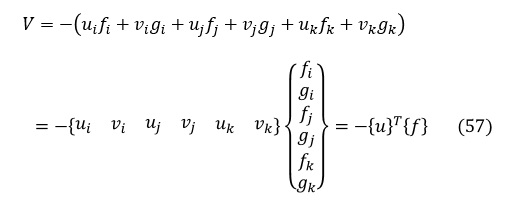
(56)式,(57)式を(51)式に代入すると,全ポテンシャルエネルギΠは次式となります。
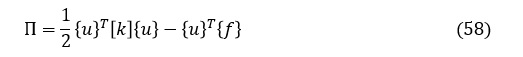
(58)式において,[k]は節点座標と材料定数(E,ν)で決まり,{f}は荷重条件として与えられるから,これらを固定して考えれば,Πは節点変位(ui,vi,uj,vj,uk,vk)によって決まります。Πの最小点を求めるにはΠの偏微分をゼロとおいて,以下に示した連立方程式を解けばよいことになります。
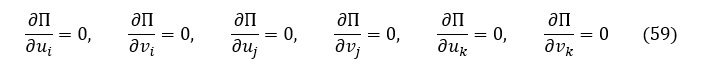
(59)式を計算していきましょう。Πを展開すると次式となります。

(59)式に従って,(60)式をui,vi,uj,vj,uk,vk で偏微分して,イコールゼロとおきます。
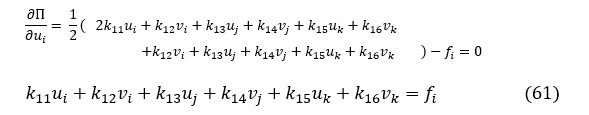
同様にして
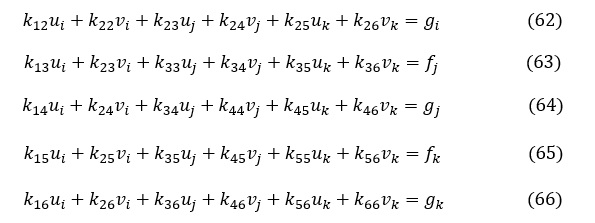
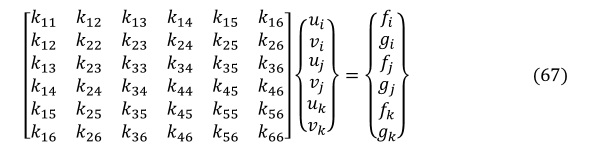
(61)式~(66)式をマトリクス表示すると次式となり,(1)式と一致します。よって,(55)式で求まる[k]は要素剛性マトリクスの各成分となります。(55)式と(47)式は一致しますので,仮想変位の原理からでも最小ポテンシャルエネルギの原理からでも,どちらからでも要素剛性マトリクスが求まりました。
参考文献
1)戸川,有限要素法概論,培風館,(S56)
2)三好,有限要素法入門,培風館,(S53)
3)O.C.ツィエンキーヴィッツ,基礎工学におけるマトリックス有限要素法,吉識,山田 監訳,(S50)

